1.2 Measuring:
Picture a person trying to bake a cake. The things he would need would be the ingredients, measuring cups and spoons and a good cake recipe. How good would his cake come out compared to someone else’s if they both used this exact same recipe?:
Picture a person trying to bake a cake. The things he would need would be the ingredients, measuring cups and spoons and a good cake recipe. How good would his cake come out compared to someone else’s if they both used this exact same recipe?:

Chocolate Cake:
Ingredients
Directions
Ingredients
- several eggs
- a couple of handfuls of flour
- a pinch of salt
- a glass of milk
- four squirts of chocolate flavoring
- two shakes of baking powder
Directions
- Mix ingredients and bake in a hot oven for a good while. Let cool.
Obviously the cakes would be very, very different. A few to most people is three, but some consider two or four a few. How big is a handful? How large is a pinch? Should you use a big glass or a little glass? How big is a squirt or a shake?
Even the directions are not clear enough. Everyone in the USA would assume that 350° is in degrees Fahrenheit. Anywhere else in the world they might think degrees Celsius. That would be three times higher than the temperature of boiling water! Also, when is it done and how long should you let it cool?
A better recipe may be:
Even the directions are not clear enough. Everyone in the USA would assume that 350° is in degrees Fahrenheit. Anywhere else in the world they might think degrees Celsius. That would be three times higher than the temperature of boiling water! Also, when is it done and how long should you let it cool?
A better recipe may be:

Chocolate Cake:
Ingredients
Directions
Ingredients
- three eggs
- four cups of flour
- 1/4 tsp. of salt
- two cups of milk
- five tablespoons of chocolate flavoring
- two teaspoons of baking powder
Directions
- Mix ingredients and bake in an oven at 350°F for half an hour. Let cool.
In science, you want the other person’s cake to be exactly like yours. This means that not only do the measurements have to be exact, but how closely you measure it should be exact. The recipe does not call for close to four cups of flour, it says four cups exactly. If your cake has 3.8 cups while I used 4.5 cups, they will be very different.

When does 1 ≠ 1.00?
In your math class, the number 1 and the number 1.00 are exactly the same. That is not true in science. If you are making measurements, it is important for you to let people know how accurate your measurement is. People need to know how precise the tool you used is. You convey that precision by the number of digits (significant figures) you record as a measurement. The more significant figures there are, the more precise the measurement.
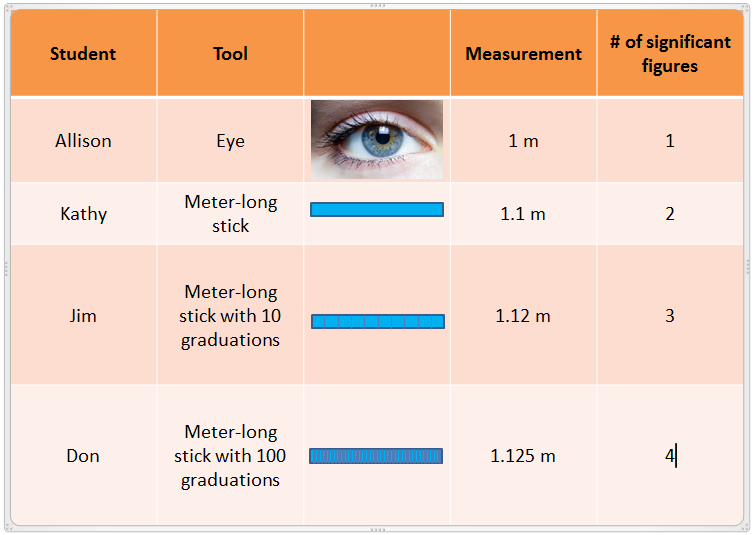
As an example, let’s say you are trying to measure the length of a coffee table. If you just look at it without using a tool, you could say it looks like it’s a meter long. You would write that as 1 m. Another person used a stick that was one meter long. She saw that the table was just a little longer than the stick. She estimated that the difference was one tenth the length of her stick. She would write that the table is 1.1 m long. A third person has a stick that is one meter in length and marked off in tenths of a meter. He lays the meter stick along the table and sees that the table is longer than the stick, but it is more than one tenth graduation on the stick. He reports the length of the table to be 1.12 m. A fourth person uses a stick marked off to 100ths of a meter (centimeters). He measures the table to be 1.125 m long.
Here are the measurements again:
In your math class, the number 1 and the number 1.00 are exactly the same. That is not true in science. If you are making measurements, it is important for you to let people know how accurate your measurement is. People need to know how precise the tool you used is. You convey that precision by the number of digits (significant figures) you record as a measurement. The more significant figures there are, the more precise the measurement.
As an example, let’s say you are trying to measure the length of a coffee table. If you just look at it without using a tool, you could say it looks like it’s a meter long. You would write that as 1 m. Another person used a stick that was one meter long. She saw that the table was just a little longer than the stick. She estimated that the difference was one tenth the length of her stick. She would write that the table is 1.1 m long. A third person has a stick that is one meter in length and marked off in tenths of a meter. He lays the meter stick along the table and sees that the table is longer than the stick, but it is more than one tenth graduation on the stick. He reports the length of the table to be 1.12 m. A fourth person uses a stick marked off to 100ths of a meter (centimeters). He measures the table to be 1.125 m long.
Here are the measurements again:
Which measurement is correct? Surprisingly, they are all correct. Each measurement is correct because it tells you not only how long the coffee table is, but also how reliable the tool is that the person used. Obviously using a meter stick gives you a better measurement than just eyeballing it. The number of significant figures that an answer has tells the reader how reliable the measurement was. The more significant figures there are, the better the measuring device.

How do you determine the number of significant figures?
With any measurement one should go to the smallest increment on the measuring device and then estimate one more from there. As an example, if a meter stick has increments to the hundredths place, then you should give a measurement to the thousandths. Every number in the measurement is accurate except the last digit. It is an estimate. Since humans read the measuring tools, and everyone is different, every measurement has an expected estimation. As an example, how long is this object? Is it 3 cm long? 3.3 cm long? 3.4 cm long? or 3.35 cm long? Make your measurement and then click or tap the image to see the answer.
With any measurement one should go to the smallest increment on the measuring device and then estimate one more from there. As an example, if a meter stick has increments to the hundredths place, then you should give a measurement to the thousandths. Every number in the measurement is accurate except the last digit. It is an estimate. Since humans read the measuring tools, and everyone is different, every measurement has an expected estimation. As an example, how long is this object? Is it 3 cm long? 3.3 cm long? 3.4 cm long? or 3.35 cm long? Make your measurement and then click or tap the image to see the answer.
Many times, zeros are not significant:
There are many measurements that are very big or very small. The mass of an electron is 0.000 000 000 000 000 000 000 000 000 911 kg. The distance to the sun is 149,000,000,000 m. Would anything be different if we wrote the distance to the sun as 149,000,000,001 m? Not really since the distance is so large, the ones place and the tens, and hundreds,… are insignificant. Knowing the measurement to that place does not help with anything. It is insignificant so we don’t include it in the measurement and place a zero there. The zero helps you know how big the measurement is, but not how accurate.
If you had really measured the distance to the sun down to the meter and it came out to 149,000,00,001 m then all those zeros had to have been measured. They were not just placed there so they are now significant.
The rules of significant figures are these:
1. All nonzero integers are significant. It had to have been measured.
2. If a zero was measured it is significant. This means that zeros between and to the right of other sig figs are significant.
3. Any zero that “pushes” the measurement away from the decimal point are not significant. These zeros are showing you the size of the number, not how precise the measurement was.
Remember, the number of significant figures in an amount helps the reader know how precise the measurement was. 1.000 liters ≠ 1 liter!
If you find this confusing, practice will help. Click or tap the link below for some on-line practice.
There are many measurements that are very big or very small. The mass of an electron is 0.000 000 000 000 000 000 000 000 000 911 kg. The distance to the sun is 149,000,000,000 m. Would anything be different if we wrote the distance to the sun as 149,000,000,001 m? Not really since the distance is so large, the ones place and the tens, and hundreds,… are insignificant. Knowing the measurement to that place does not help with anything. It is insignificant so we don’t include it in the measurement and place a zero there. The zero helps you know how big the measurement is, but not how accurate.
If you had really measured the distance to the sun down to the meter and it came out to 149,000,00,001 m then all those zeros had to have been measured. They were not just placed there so they are now significant.
The rules of significant figures are these:
1. All nonzero integers are significant. It had to have been measured.
2. If a zero was measured it is significant. This means that zeros between and to the right of other sig figs are significant.
3. Any zero that “pushes” the measurement away from the decimal point are not significant. These zeros are showing you the size of the number, not how precise the measurement was.
Remember, the number of significant figures in an amount helps the reader know how precise the measurement was. 1.000 liters ≠ 1 liter!
If you find this confusing, practice will help. Click or tap the link below for some on-line practice.