5.4 - Energy Conversion and Work
Remember that energy can neither be created nor destroyed. It can only be transferred and/or transformed. This means that throughout any interaction, all of the energy that was in the system, has to be accounted for.
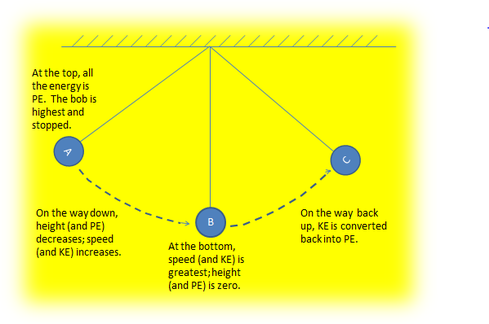
A useful model of energy transformation is the pendulum. Once it begins its swing, the pendulum constantly converts PE to KE, back to PE, then to KE, …
At the top of the pendulum’s swing, the bob (Yes, that’s what the weight is called!) is stopped. Therefore, at those points it has no kinetic energy. At the bottom of the pendulum’s swing, the bob has zero height. Therefore, it has zero potential energy at that point. In between those points, the bob has a mix of both potential and kinetic energies.
The sum of the potential and kinetic energies must always add up to the amount of energy originally put into the system to lift the bob up. That original energy is called the work.
During any type of interaction, energy is transferred and/or transformed. When an object gains energy, work is being done to that object. The term work is much more specific in physics than anywhere else. For work to be done a force must be applied through a distance. The relationship is stated like this:
A useful model of energy transformation is the pendulum. Once it begins its swing, the pendulum constantly converts PE to KE, back to PE, then to KE, …
At the top of the pendulum’s swing, the bob (Yes, that’s what the weight is called!) is stopped. Therefore, at those points it has no kinetic energy. At the bottom of the pendulum’s swing, the bob has zero height. Therefore, it has zero potential energy at that point. In between those points, the bob has a mix of both potential and kinetic energies.
The sum of the potential and kinetic energies must always add up to the amount of energy originally put into the system to lift the bob up. That original energy is called the work.
During any type of interaction, energy is transferred and/or transformed. When an object gains energy, work is being done to that object. The term work is much more specific in physics than anywhere else. For work to be done a force must be applied through a distance. The relationship is stated like this:
The unit of force is the Newton and the unit of distance is the meter. Therefore, the unit of work is the Newton•meter. That is a Joule (J)! Remember that the unit of energy is also the Joule. This means that energy can be defined as the ability to do work. When work is done on an object, its energy changes.

As another example, if a person were to lift a 1470 N weight up 2 m, he would have done (1470 N X 2 m =) 2940 J of work. You know that if an object moves up, its gravitational potential energy has increased. In this case it has gained (150 kg X 9.8 N/Kg X 2.0 m =) 2940 J of potential energy. The work has become potential.
If a person were holding a 1470 N weight at a height of 2 m no work is being done to that weight. The force is not being applied through a distance. If there is no change in position then Δd = 0 and Work = 0. Another way to look at it is that since the position of the object has not changed, its potential energy has not changed. If there is no change in energy to the object, work must not have been done.
If a person were holding a 1470 N weight at a height of 2 m no work is being done to that weight. The force is not being applied through a distance. If there is no change in position then Δd = 0 and Work = 0. Another way to look at it is that since the position of the object has not changed, its potential energy has not changed. If there is no change in energy to the object, work must not have been done.
A definition of work that states there must be a change of energy also works when discussing kinetic energy. If an object at rest has a constant force applied to it, that object will accelerate. Over the distance that the force is applied, the object’s velocity will increase. The faster the object is going, the more kinetic energy it has. That energy came from the work that was done to the object.
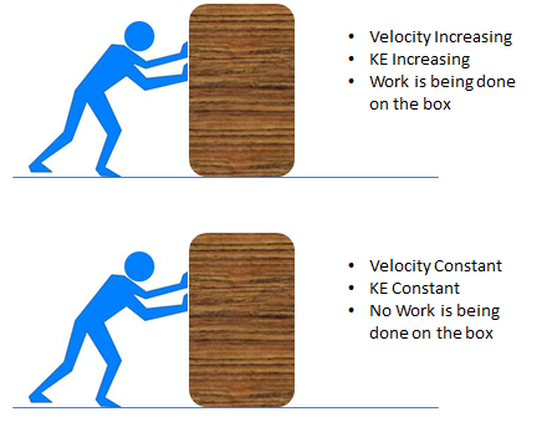
If a force is applied to an object and the object continues to move at a constant velocity is work being done? By one definition, W = F x Δd, work is being done. By our other definition (work causes a change in an object’s energy) work is not being done. Which one is it?
If a force is applied to an object and the object continues to move at a constant velocity is work being done? By one definition, W = F x Δd, work is being done. By our other definition (work causes a change in an object’s energy) work is not being done. Which one is it?
Both are correct to some extent. The person pushing the box is doing Work in this situation- applying a force through a distance. However, Friction is also doing Work on the box - applying a force through a distance resisting the motion of the box. Since the Kinetic Energy of the box is not changing, overall, there is no work being done on the box.