3.6 Free Fall

On October 14, 2012, Austrian Felix Baumgartner stepped out of a capsule 127,852 feet above the Earth and, he fell. He was so high in the atmosphere that there was essentially no air for him to breathe so he had to wear a space suit. There was also so little air that air resistance was negligible therefore gravity was the only force acting on him. When gravity is the only force acting on an object, that object is said to be in Free Fall.
As Baumgartner fell towards Earth, he moved deeper into the atmosphere and air resistance became more pronounced. Once air resistance entered the mix, he was no longer in Free Fall. Nevertheless, during the fall he still achieved a top speed of 843.6 miles per hour. He is the only human ever to have traveled faster than the speed of sound unaided by a vehicle.
As Baumgartner fell towards Earth, he moved deeper into the atmosphere and air resistance became more pronounced. Once air resistance entered the mix, he was no longer in Free Fall. Nevertheless, during the fall he still achieved a top speed of 843.6 miles per hour. He is the only human ever to have traveled faster than the speed of sound unaided by a vehicle.
As long as air resistance can be ignored, objects near the surface of Earth fall at a constant acceleration of 10 m/s/s (the actual value is 9.8 m/s/s but, 10 m/s/s is close enough for our purposes). This "special" acceleration is written as g. (NOTE: g decreases with height above the Earth. At his initial elevation of 127,852 feet, g for Felix Baumgartner would have been 9.73 m/s/s).
Since, under routine conditions, g near the surface of the Earth is fairly constant, Free Fall can be conveniently used to study problems involving constant acceleration.
Since, under routine conditions, g near the surface of the Earth is fairly constant, Free Fall can be conveniently used to study problems involving constant acceleration.
Free Fall: How Fast?

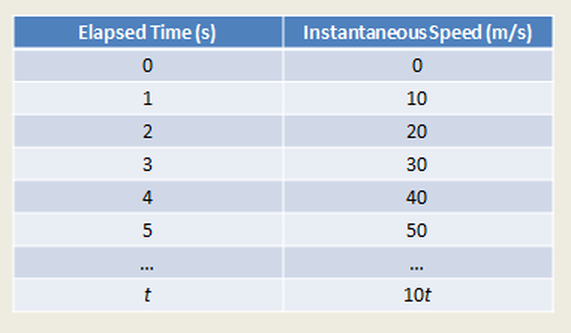
Picture a bowling ball equipped with a speedometer. (The speedometer would measure the instantaneous velocity of the bowling ball). If you took this bowling ball to a high cliff and dropped it, how fast would it be moving after 1 second? 2 seconds? 5 seconds? Since we know that the ball will fall with an acceleration of 9.8 m/s/s (air resistance is negligible), this means that it will gain approximately 10 m/s of speed for every second it falls. Look at the table below:
This leads us to the relationship: g = v/t or v = gt
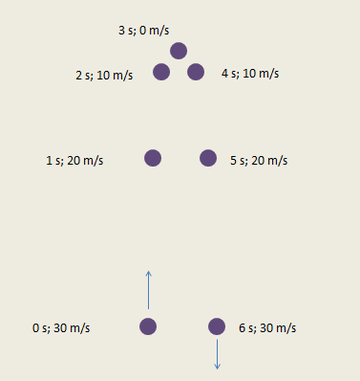
This does a good job of explaining how the speed of a dropped (initial velocity of zero) ball changes, but what if the ball is traveling upward initially?
Gravity only does one thing: pull downward. Just as gravity will cause an object to speed up downward if you drop it, it will also slow the object down if it is thrown or launched upward.
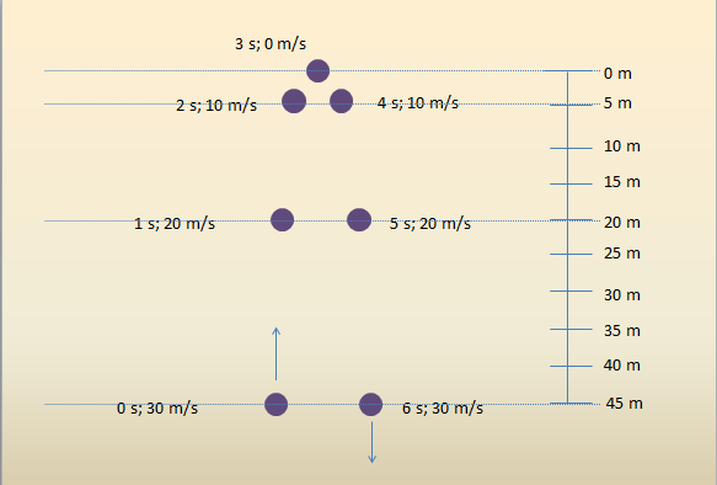
If the ball to the left is launched upward with a speed of 30 m/s, after 1 second, it will be traveling 10 m/s slower. After two seconds, it will have lost 20 m/s. After 3 seconds it will have lost 30 m/s. For a brief moment, its instantaneous velocity will be zero and then the downward trip begins and it gains speed at the same rate at which it lost speed on the way up. If an object in Free Fall has an initial velocity, its final velocity can be calculated using the equation vf = vi + gt. This works for all situations because, if the object starts from rest, just plug in zero for vi.
Gravity only does one thing: pull downward. Just as gravity will cause an object to speed up downward if you drop it, it will also slow the object down if it is thrown or launched upward.
If the ball to the left is launched upward with a speed of 30 m/s, after 1 second, it will be traveling 10 m/s slower. After two seconds, it will have lost 20 m/s. After 3 seconds it will have lost 30 m/s. For a brief moment, its instantaneous velocity will be zero and then the downward trip begins and it gains speed at the same rate at which it lost speed on the way up. If an object in Free Fall has an initial velocity, its final velocity can be calculated using the equation vf = vi + gt. This works for all situations because, if the object starts from rest, just plug in zero for vi.
Free Fall: How Far?
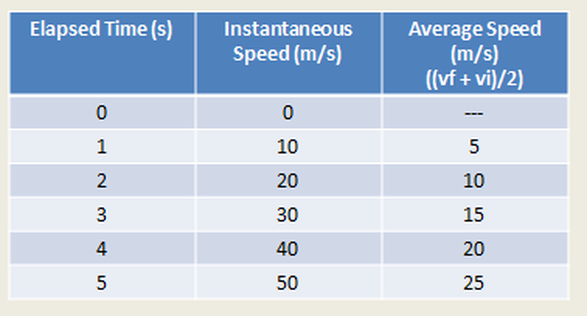
Let's look again at Table 3.6.1 above. When the bowling ball is dropped from rest, exactly 1 second later, it is traveling 10 m/s. The average velocity during that first one second time interval would be 5 m/s (initial velocity + final velocity)/2. After 2 seconds, the bowling ball is traveling 20 m/s. The average velocity for that two second time interval is 10 m/s. We can do this for each time interval resulting in the chart below.
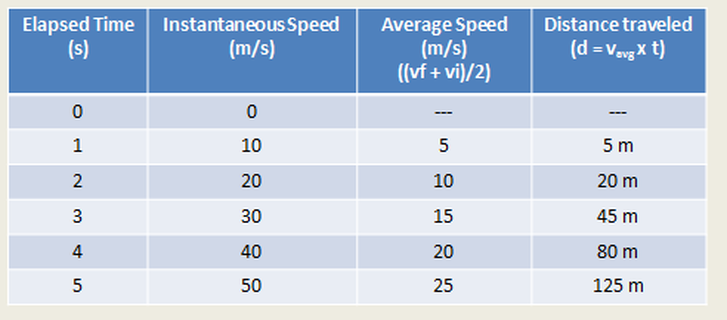
Finally, if we want to figure out How Far the bowling ball has fallen, we simply use the relationship d = v x t and use the Average Velocity for v.
This is what it looks like when we put How Fast and How Far together with the upwardly thrown ball:
Kinematic Equations
Use the following equations when solving Motion Problems. Remember, if an object is accelerating, you must use an equation that includes acceleration. Also remember to use g (10 m/s/s) as the acceleration if the object is in Free Fall.